For computer vision The code for this post can be found here. tasks MishDiganta Misra. 2019. Mish: A self regularized non-monotonic neural activation function. arXiv:1908.08681. is my go to activation function. When training new models or new layers during transfer learning, I have found that Mish performs on par if not better then alternative activation functions.
The primary downside of using Mish has been performance. The PyTorch JIT versions have often been slower than other PyTorch native activation functions. While it was possible to achieve similar performance to a native activation function it required installing a CUDA implementation which isn’t possible on every platformSuch as Kaggle Notebooks..
When Diganta Misra announced that Mish would have a native implementation in PyTorch 1.9, I hoped it would it would match or exceed the computational performance of Thomas Brandon’s MishCuda implementation. And after 1.9’s release, decided to benchmark it to find out.
But first, some background on Mish and activation functionsTo skip directly to the benchmark, click here..
# Activation Functions
Activation functions are a necessary part of neural networks as they add non-linearities to an otherwise linear network which allows them to learn non-linear complex functions. Without activation functions, neural networks would be very high polynomial linear functions and training models would be akin to fitting a linear regression.
Early on, neural networks used Sigmoid or TanH as their activation functions but transitioned to Rectified Linear Unit (ReLU)Xavier Glorot, Antoine Bordes, and Yoshua Bengio. 2011. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, PMLR, 315–323. which has remained the default activation function across many models and papers due to its simplicity and consistent performance across most tasksIn some domains, such as tabular neural networks, ReLU is still one of the best activation functions, not just the default..
Mathematically, ReLU is defined as:
with a plot of ReLU is shown in Figure 1 below.
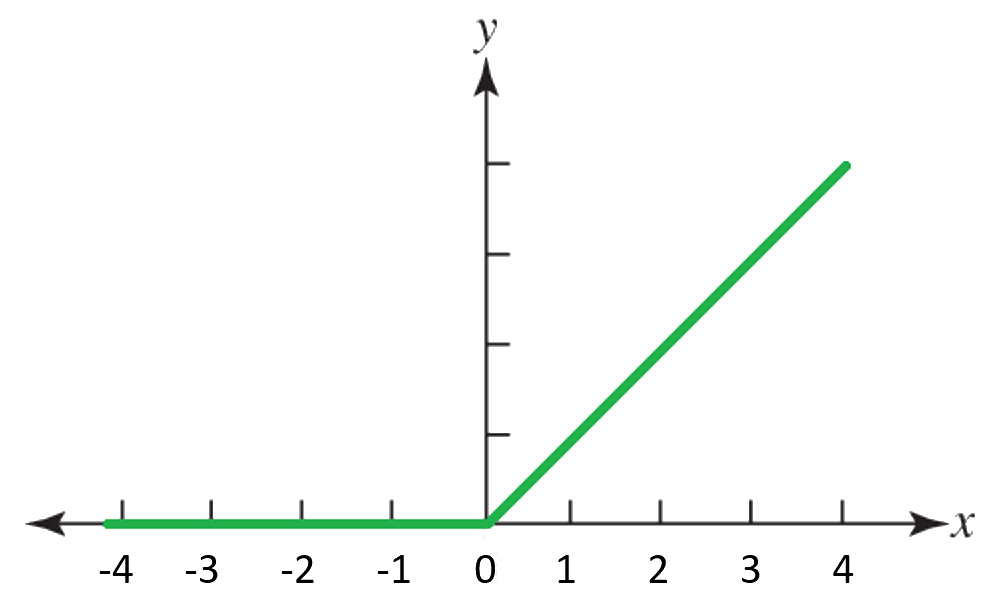
ReLU has a few weaknesses which have spurred the hunt for better activation functions. The discontinuous derivative and flat nonlinear function for negative values creates an output landscape with sharp transitions and a rough profile, which can cause undesired outcomes during gradient-based optimization.

One possible negative outcome is the Dying ReLU problem, where the information loss of negative inputs being zeroed prevents gradient updates from flowing through the network during backpropagation; leading to stagnant and unchanged weights. In a worst case scenario this results in a large portion of the model unable to learn further. Fortunately, a properly calibrated learning rate can prevent this problem from occurring.
# Mish
Mish is a self-gated, smooth, continuously differentiable, and nonmonotonic activation function. Mish is defined as:
where Qian Liu and Steve Furber. 2016. Noisy Softplus: A Biology Inspired Activation Function. In Neural Information Processing. DOI:10.1007/978-3-319-46681-1_49 is . It is bounded below and unbounded above with a range of . Mish was inspiredMisra cites Swish as the inspiration for Mish, however as Swish is SiLU but with a trainable β parameter which is usually set to 1 (making it identical to SiLU), I will refer to Swish as SiLU. by SiLUStefan Elfwing, Eiji Uchibe, and Kenji Doya. Sigmoid-Weighted Linear Units for Neural Network Function Approximation in Reinforcement Learning. arXiv:1702.03118. which shares many similar properties.
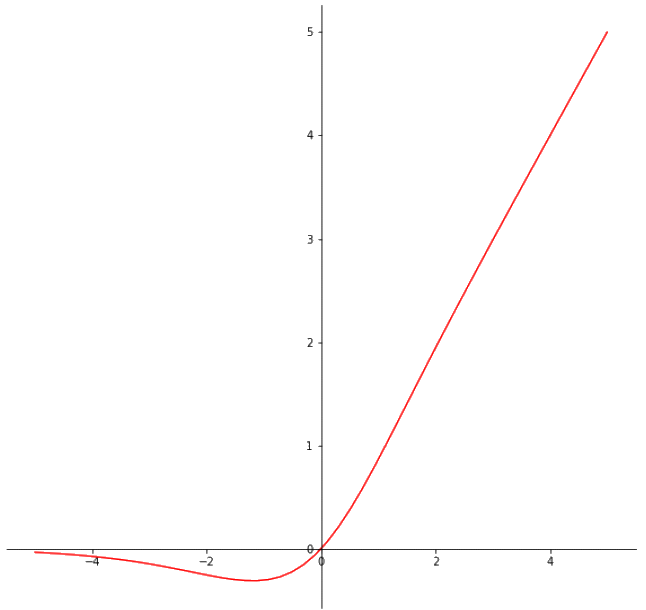
All of these properties combined—self-gated, smooth, continuously differentiable, unbounded above, bounded below, and nonmonotonic—give Mish advantages over other activation functions such as ReLU.
Inspired by Long Short-Term Memory (LSTMs)Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long Short-Term Memory. Neural Computation 9, 8 (November 1997), 1735–1780. DOI:10.1162/neco.1997.9.8.1735 and similar architectures’ gate structures, self-gating allows Mish to modulate its input by using the input as a gate to multiply with the output of the non-linear function of the input. Additionally, it allows Mish to be a drop-in replacement for non-gated activation functions, as Mish only requires a single input verses a traditional gate’s requirement of multiple inputs.
Mish’s smooth profile assists in better gradient flow, which allows for easier updates during backpropagation. In addition to being smooth, Mish’s continuous differentiability means Mish avoids singularities in its derivative which can hinder gradient-based optimization.
Mish is unbounded above which prevents saturation, that is unnecessarily slowing down training due to near-zero gradients, a feature it shares with ReLU. Mish is bounded below which gives it strong regularization effects during training. But unlike ReLU, Mish allows a small amount of negative outputs to pass through, which eliminates the Dying ReLU problem and leads to improved information propagation throughout the network. This gives Mish its nonmonotonic property and allows it to achieve superior performance in very deep networks to monotonic activation functions.

Figure 4 shows how these properties create a smooth output landscape with smooth transitions. A stark visual contrast to ReLU as shown in Figure 2.
Since Mish’s introduction, Mish has been benchmarked in numerous vision tasks with far more wins than losses, including outperforming SiLU in 75% of these tasks. Mish has been used in models such as YOLOv4Alexey Bochkovskiy, Chien-Yao Wang, and Hong-Yuan Mark Liao. 2020. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv:2004.10934. which currently is state of the art for real-time object detection on MSCOCO, it was found to have similar adversarial robustness to GELUDan Hendrycks and Kevin Gimpel. 2020. Gaussian Error Linear Units (GELUs). arXiv:1606.08415., and the paper was accepted in the prestigious British Machine Vision Conference 2020. Mish was also used by the fast.ai community to achieve state of the art accuracy on the Imagenette leaderboard, which is where I first learned about it.
# Benchmarking
To benchmark PyTorch native Mish’s performance against other implementations and activation functions, I tested ReLU, Leaky ReLUAndrew L. Maas, Awni Y. Hannun, and Andrew Y. Ng. 2013. Rectifier nonlinearities improve neural network acoustic models. In ICML Workshop on Deep Learning for Audio, Speech and Language Processing., Softplus, SiLU, and Mish via the following implementations:
- ReLU: PyTorch’s native implementation
- Leaky ReLU: PyTorch’s native implementation
- Softplus: PyTorch’s native implementation
- SiLU (jit): fast.ai’s Torchscript implementation
- SiLU (native): PyTorch’s native implementation
- Mish (naive): a plain PyToch implementation
- Mish (jit): fast.ai’s Torchscript implementation
- Mish (cuda): Thomas Brandon’s CUDA implementation
- Mish(native): PyTorch’s native implementation
To measure the computational performance of all nine activation function implementations on Google Colab using their Tesla V100, Tesla P100, and CPU instances, I lightly modified Thomas Brandon’s CUDA benchmarking script. The script uses a rank four tensor of size (16,10,256,256)I also benchmarked computational performance on a rank four tensor of size (64,10,256,256), but did not reproduce the results as they tell the same story. and records 100 forward and backward passes after 10 warmup runs. My version adds bfloat16 to the list of float16, float32, and float64 tensor types and a CPU benchmark where I only measured float32 performance. I additionally ran a PyTorch 1.8 test on a Tesla V100 to see if there have been changes in other activation function implementation performance across PyTorch versions.
All results are using CUDA 10.2.
Code and raw results for all benchmarks are available here.
# V100
On a Tesla V100, PyTorch native Mish’s performance is competitive with all other activation functions and implementations, if not the outright leader. For example, during Mixed Precision training Mish should have the fastest forward pass and should only be outperformed during the backward pass by SiLU. On Volta hardware native Mish is a clear winner over other Mish implementations, and I would be surprised if this lead did not hold on modern Ampere hardware too.
Given the complexity differences, one surprising result is the performance of Mish and SiLU relative to ReLU. With the exception of float64, native Mish is faster than native ReLU, and native SiLU is always faster than native ReLU.
Activation Functions’ Forward and Backward Pass on a Tesla V100-SXM2-16GB using PyTorch 1.9.
| Forward Pass | Backward Pass | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Tensor Type | Function | Mean | StDev | Min | Max | Mean | StDev | Min | Max |
| float16 | ReLU | 100.4µs | 4.316µs | 96.26µs | 116.7µs | 179.6µs | 16.79µs | 161.8µs | 301.1µs |
| Leaky ReLU | 95.32µs | 3.966µs | 92.16µs | 120.8µs | 178.8µs | 28.97µs | 158.7µs | 323.6µs | |
| Softplus | 105.4µs | 7.069µs | 100.4µs | 151.6µs | 237.3µs | 378.3µs | 171.0µs | 3.813ms | |
| SiLU (jit) | 114.3µs | 62.76µs | 99.33µs | 638.0µs | 249.7µs | 288.3µs | 169.0µs | 2.765ms | |
| SiLU (native) | 86.78µs | 2.632µs | 83.97µs | 100.4µs | 158.8µs | 12.15µs | 147.5µs | 196.6µs | |
| Mish (naive) | 239.4µs | 7.391µs | 232.4µs | 272.4µs | 502.3µs | 341.5µs | 463.9µs | 3.900ms | |
| Mish (jit) | 187.0µs | 4.837µs | 182.3µs | 204.8µs | 254.5µs | 9.229µs | 248.8µs | 328.7µs | |
| Mish (cuda) | 116.1µs | 5.289µs | 107.5µs | 136.2µs | 185.1µs | 21.07µs | 169.0µs | 291.8µs | |
| Mish (native) | 84.57µs | 3.283µs | 81.92µs | 101.4µs | 168.2µs | 16.51µs | 155.6µs | 271.4µs | |
| bfloat16 | ReLU | 94.56µs | 65.80µs | 83.97µs | 747.5µs | 197.6µs | 246.0µs | 143.4µs | 1.988ms |
| Leaky ReLU | 84.14µs | 5.659µs | 80.90µs | 116.7µs | 155.2µs | 13.22µs | 143.4µs | 199.7µs | |
| Softplus | 97.58µs | 3.035µs | 95.23µs | 109.6µs | 152.3µs | 13.03µs | 146.4µs | 261.1µs | |
| SiLU (jit) | 178.3µs | 7.874µs | 172.0µs | 213.0µs | 598.2µs | 412.6µs | 542.7µs | 4.677ms | |
| SiLU (native) | 84.90µs | 4.708µs | 80.90µs | 113.7µs | 187.3µs | 162.1µs | 144.4µs | 1.535ms | |
| Mish (naive) | 242.1µs | 5.280µs | 236.5µs | 262.1µs | 472.0µs | 70.70µs | 458.8µs | 1.011ms | |
| Mish (jit) | 258.8µs | 39.72µs | 247.8µs | 647.2µs | 796.5µs | 265.8µs | 758.8µs | 3.290ms | |
| Mish (cuda) | 258.8µs | 39.72µs | 247.8µs | 647.2µs | 796.5µs | 265.8µs | 758.8µs | 3.290ms | |
| Mish (native) | 87.34µs | 5.521µs | 82.94µs | 119.8µs | 170.9µs | 21.28µs | 154.6µs | 332.8µs | |
| float32 | ReLU | 132.7µs | 5.097µs | 128.0µs | 149.5µs | 235.3µs | 124.5µs | 216.1µs | 1.331ms |
| Leaky ReLU | 134.6µs | 53.66µs | 123.9µs | 663.6µs | 291.6µs | 416.3µs | 216.1µs | 3.420ms | |
| Softplus | 127.1µs | 3.866µs | 123.9µs | 144.4µs | 219.1µs | 3.852µs | 217.1µs | 254.0µs | |
| SiLU (jit) | 305.7µs | 101.5µs | 288.8µs | 1.312ms | 974.2µs | 201.2µs | 932.9µs | 2.338ms | |
| SiLU (native) | 127.4µs | 4.018µs | 122.9µs | 144.4µs | 217.9µs | 754.2ns | 216.1µs | 220.2µs | |
| Mish (naive) | 396.4µs | 71.03µs | 382.0µs | 1.080ms | 912.2µs | 748.6µs | 819.2µs | 8.176ms | |
| Mish (jit) | 408.6µs | 40.85µs | 395.3µs | 805.9µs | 1.410ms | 846.5µs | 1.294ms | 9.495ms | |
| Mish (cuda) | 141.0µs | 4.121µs | 135.2µs | 158.7µs | 235.6µs | 77.05µs | 222.2µs | 969.7µs | |
| Mish (native) | 128.3µs | 2.898µs | 124.9µs | 139.3µs | 220.5µs | 952.9ns | 219.1µs | 224.3µs | |
| float64 | ReLU | 324.0µs | 4.909µs | 318.5µs | 341.0µs | 492.1µs | 170.1µs | 470.0µs | 2.169ms |
| Leaky ReLU | 319.6µs | 4.031µs | 314.4µs | 334.8µs | 472.4µs | 2.247µs | 469.0µs | 485.4µs | |
| Softplus | 312.7µs | 4.179µs | 307.2µs | 329.7µs | 470.3µs | 1.141µs | 468.0µs | 473.1µs | |
| SiLU (jit) | 722.5µs | 9.100µs | 712.7µs | 756.7µs | 2.447ms | 172.7µs | 2.416ms | 4.107ms | |
| SiLU (native) | 316.3µs | 5.669µs | 310.3µs | 348.2µs | 473.1µs | 1.782µs | 470.0µs | 482.3µs | |
| Mish (naive) | 995.5µs | 18.37µs | 985.1µs | 1.165ms | 1.999ms | 79.57µs | 1.979ms | 2.789ms | |
| Mish (jit) | 1.009ms | 10.14µs | 997.4µs | 1.050ms | 3.405ms | 178.1µs | 3.374ms | 5.177ms | |
| Mish (cuda) | 344.1µs | 5.212µs | 340.0µs | 371.7µs | 470.1µs | 1.002µs | 469.0µs | 476.2µs | |
| Mish (native) | 334.5µs | 4.198µs | 328.7µs | 348.2µs | 479.5µs | 1.436µs | 478.2µs | 489.5µs | |
Lower is better. Fastest pass and those statistically indistinguishable at the p=0.001 level are highlighted.
# P100
Unlike the Tesla V100, the Tesla P100 had wide variance in computational performance for many activation functions. The large variance for the bfloat16, float32, and float64 backward pass caused the computational time of many of these activation functions to be statistically indistinguishable from each other at the p=0.001 level. Changing the number of timed iterations from 100 to 50 & 25 and warmup runs from 10 to 5 did not materially change the variance of the tests.
Focusing on float16 where there is less variance, PyTorch’s native Mish had a significant improvement over other Mish implementations but its performance still lags most of the other PyTorch native activation functions, with the notable exception of Softplus, which brings up the rear.
Despite these results, native Mish is either more performant or statistically indistinguishable from other Mish implementations.
Activation Functions’ Forward and Backward Pass on a Tesla P100-PCIE-16GB using PyTorch 1.9.
| Forward Pass | Backward Pass | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Tensor Type | Function | Mean | StDev | Min | Max | Mean | StDev | Min | Max |
| float16 | ReLU | 114.3µs | 15.35µs | 106.2µs | 236.0µs | 401.8µs | 502.5µs | 327.6µs | 5.170ms |
| Leaky ReLU | 104.9µs | 15.58µs | 101.1µs | 257.4µs | 316.7µs | 15.29µs | 314.0µs | 468.8µs | |
| Softplus | 225.3µs | 61.01µs | 214.5µs | 831.2µs | 449.3µs | 65.98µs | 436.4µs | 1.091ms | |
| SiLU (jit) | 181.8µs | 21.29µs | 177.0µs | 363.1µs | 364.7µs | 769.8ns | 362.7µs | 366.6µs | |
| SiLU (native) | 128.5µs | 4.818µs | 124.5µs | 148.4µs | 333.0µs | 183.8µs | 309.5µs | 2.113ms | |
| Mish (naive) | 434.0µs | 25.70µs | 428.3µs | 686.8µs | 932.5µs | 213.1µs | 900.4µs | 2.707ms | |
| Mish (jit) | 378.0µs | 7.118µs | 368.3µs | 400.0µs | 625.6µs | 307.2µs | 590.4µs | 3.681ms | |
| Mish (cuda) | 277.4µs | 3.832µs | 273.4µs | 305.4µs | 478.6µs | 467.8ns | 477.8µs | 480.2µs | |
| Mish (native) | 206.1µs | 44.46µs | 197.5µs | 644.7µs | 446.4µs | 26.33µs | 441.5µs | 678.7µs | |
| bfloat16 | ReLU | 107.4µs | 2.817µs | 105.2µs | 119.2µs | 307.4µs | 5.838µs | 305.6µs | 359.3µs |
| Leaky ReLU | 103.2µs | 3.106µs | 100.8µs | 122.3µs | 307.4µs | 2.372µs | 306.5µs | 330.7µs | |
| Softplus | 240.4µs | 32.73µs | 235.0µs | 563.8µs | 429.4µs | 328.5µs | 395.8µs | 3.698ms | |
| SiLU (jit) | 273.8µs | 6.896µs | 268.6µs | 311.7µs | 909.9µs | 114.8µs | 896.0µs | 2.052ms | |
| SiLU (native) | 143.6µs | 5.667µs | 138.5µs | 175.3µs | 360.0µs | 235.9µs | 314.3µs | 2.393ms | |
| Mish (naive) | 463.9µs | 61.92µs | 454.0µs | 1.079ms | 884.3µs | 212.4µs | 861.4µs | 2.998ms | |
| Mish (jit) | 472.1µs | 5.339µs | 467.2µs | 490.6µs | 1.371ms | 283.2µs | 1.329ms | 3.923ms | |
| Mish (cuda) | 472.1µs | 5.339µs | 467.2µs | 490.6µs | 1.371ms | 283.2µs | 1.329ms | 3.923ms | |
| Mish (native) | 218.0µs | 12.73µs | 212.5µs | 338.4µs | 511.6µs | 231.6µs | 453.4µs | 1.670ms | |
| float32 | ReLU | 189.9µs | 47.20µs | 182.3µs | 658.5µs | 468.4µs | 258.1µs | 441.3µs | 3.037m |
| Leaky ReLU | 185.1µs | 40.48µs | 177.8µs | 586.2µs | 471.9µs | 223.4µs | 441.4µs | 2.584ms | |
| Softplus | 208.0µs | 47.14µs | 197.9µs | 674.7µs | 465.0µs | 215.5µs | 442.1µs | 2.609ms | |
| SiLU (jit) | 433.0µs | 27.39µs | 423.3µs | 698.0µs | 1.574ms | 286.1µs | 1.525ms | 4.144ms | |
| SiLU (native) | 181.3µs | 6.474µs | 176.3µs | 224.7µs | 447.2µs | 40.24µs | 441.3µs | 847.6µs | |
| Mish (naive) | 595.9µs | 19.62µs | 586.6µs | 773.0µs | 1.365ms | 69.41µs | 1.352ms | 1.946ms | |
| Mish (jit) | 605.0µs | 6.587µs | 599.2µs | 641.4µs | 2.148ms | 401.9µs | 2.090ms | 5.812ms | |
| Mish (cuda) | 283.4µs | 4.760µs | 278.7µs | 300.0µs | 490.5µs | 21.11µs | 485.7µs | 700.1µs | |
| Mish (native) | 208.9µs | 40.96µs | 199.9µs | 610.7µs | 497.6µs | 218.6µs | 466.3µs | 2.442ms | |
| float64 | ReLU | 392.7µs | 4.992µs | 386.7µs | 415.8µs | 721.7µs | 204.1µs | 694.0µs | 2.732ms |
| Leaky ReLU | 390.2µs | 8.284µs | 382.8µs | 447.1µs | 707.8µs | 79.32µs | 694.6µs | 1.455ms | |
| Softplus | 489.0µs | 16.10µs | 482.1µs | 636.3µs | 813.3µs | 180.5µs | 783.9µs | 2.473ms | |
| SiLU (jit) | 1.006ms | 6.768µs | 995.1µs | 1.026ms | 3.258ms | 112.6µs | 3.239ms | 4.378ms | |
| SiLU (native) | 382.9µs | 7.561µs | 377.0µs | 435.7µs | 692.6µs | 2.279µs | 688.0µs | 709.7µs | |
| Mish (naive) | 1.343ms | 8.757µs | 1.332ms | 1.403ms | 2.828ms | 390.0µs | 2.766ms | 5.945ms | |
| Mish (jit) | 1.355ms | 6.540µs | 1.346ms | 1.385ms | 4.575ms | 212.3µs | 4.541ms | 6.687ms | |
| Mish (cuda) | 717.0µs | 4.584µs | 713.2µs | 746.3µs | 976.7µs | 611.9ns | 975.2µs | 979.6µs | |
| Mish (native) | 645.9µs | 5.989µs | 639.8µs | 669.6µs | 976.7µs | 201.0µs | 943.0µs | 2.408ms | |
Lower is better. Fastest pass and those statistically indistinguishable at the p=0.001 level are highlighted.
# CPU
The CPUs which Google Colab serves on their instances are variable from generation to generation. I was able to run the CPU benchmarkYou shouldn’t train neural networks on CPU, but just in case I timed the backward pass in addition to the forward pass to benchmark inference. on Haswell, Broadwell, and SkylakeIntel has multiple product generations, Skylake, Cascade Lake, and Cooper Lake, which all share the same Family 6 Model 85 designation, but due to the cache size I think I benchmarked on a Skylake. Xeon CPUs. There were not any major differences between CPU generations, other than older CPUs being slower, so I only reproduced the Haswell and Skylake results.
Unsurprising due to its simplicity, ReLU has the fastest forward pass across all tested CPU generations. The surprising result is PyTorch native Mish is significantly slower than all other activation functions. A result replicated across all tested CPU generations. A priori, I would have expected it to perform on par with native SiLU, but Mish is an order of magnitude slower. The other intriguing result is a backward pass using Softplus was faster than a forward pass. This oddity persisted across multiple runs on all CPU generations.
When using CPU for inference, it would be best to replace the native Mish version with the TorchScript version. At least until PyTorch improves the CPU optimizes for native Mish.
Activation Functions’ Forward and Backward Pass on a Haswell and Skylake Xeon using PyTorch 1.9
| Forward Pass | Backward Pass | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CPU | Function | Mean | StDev | Min | Max | Mean | StDev | Min | Max |
| Haswell | ReLU | 19.95ms | 618.7µs | 18.61ms | 23.66ms | 44.59ms | 1.026ms | 42.70ms | 49.14ms |
| Leaky ReLU | 20.60ms | 850.2µs | 17.80ms | 25.07ms | 45.02ms | 1.071ms | 42.83ms | 48.56ms | |
| Softplus | 61.69ms | 1.328ms | 59.94ms | 65.84ms | 49.82ms | 1.341ms | 48.06ms | 56.02ms | |
| SiLU (jit) | 47.55ms | 2.001ms | 44.50ms | 53.54ms | 168.6ms | 2.993ms | 162.4ms | 181.5ms | |
| SiLU (native) | 24.50ms | 1.224ms | 22.62ms | 30.06ms | 50.89ms | 1.382ms | 48.49ms | 58.31ms | |
| Mish (naive) | 123.6ms | 2.575ms | 120.1ms | 132.6ms | 143.0ms | 2.669ms | 138.1ms | 154.2ms | |
| Mish (jit) | 123.0ms | 2.387ms | 120.1ms | 132.0ms | 292.3ms | 3.622ms | 284.6ms | 301.6ms | |
| Mish (native) | 144.5ms | 1.294ms | 142.3ms | 149.8ms | 183.0ms | 2.418ms | 178.8ms | 192.1ms | |
| Skylake | ReLU | 9.791ms | 541.3µs | 9.225ms | 13.19ms | 26.25ms | 808.5µs | 25.39ms | 29.88ms |
| Leaky ReLU | 10.69ms | 664.5µs | 9.579ms | 13.68ms | 28.27ms | 1.210ms | 26.49ms | 31.89ms | |
| Softplus | 48.18ms | 2.954ms | 43.05ms | 53.93ms | 32.99ms | 2.090ms | 30.05ms | 40.69ms | |
| SiLU (jit) | 27.55ms | 1.636ms | 25.81ms | 34.08ms | 95.21ms | 2.974ms | 91.30ms | 105.0ms | |
| SiLU (native) | 13.83ms | 687.5µs | 13.23ms | 17.85ms | 30.66ms | 1.096ms | 29.63ms | 35.38ms | |
| Mish (naive) | 74.72ms | 5.135ms | 68.01ms | 85.55ms | 84.82ms | 3.569ms | 78.94ms | 94.52ms | |
| Mish (jit) | 73.17ms | 4.608ms | 67.65ms | 85.18ms | 170.3ms | 7.535ms | 160.6ms | 189.9ms | |
| Mish (native) | 113.9ms | 7.488ms | 103.4ms | 129.7ms | 142.7ms | 9.413ms | 130.2ms | 164.6ms | |
Lower is better. All results for float32. Fastest pass and those statistically indistinguishable at the p=0.001 level are highlighted.
# PyTorch 1.8 V100
PyTorch did not have a native implementation of Mish in version 1.8, so this test is to see how much variance there is in activation function performance from PyTorch version to PyTorch version. Most PyTorch 1.8 activation functions are either statistically indistinguishable at the p=0.001 level or are slower than their PyTorch 1.9 counterparts. Native SiLU’s forward pass had a noticeably consistent improvement in speed from PyTorch 1.8 to PyTorch 1.9.
One notable exception is the forward pass of native ReLU, which had a statistically significant decrease in performance for both float16 and float32 from PyTorch 1.8 to PyTorch 1.9.
Activation Functions’ Forward and Backward Pass on a Tesla V100-SXM2-16GB using PyTorch 1.8.
| Forward Pass | Backward Pass | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Tensor Type | Function | Mean | StDev | Min | Max | Mean | StDev | Min | Max |
| float16 | ReLU | 96.16µs | 2.513µs | 94.21µs | 107.5µs | 174.2µs | 10.19µs | 159.7µs | 217.1µs |
| Leaky ReLU | 99.91µs | 23.17µs | 88.06µs | 293.9µs | 248.1µs | 421.7µs | 155.6µs | 3.763ms | |
| Softplus | 99.59µs | 3.792µs | 96.26µs | 120.8µs | 192.7µs | 179.1µs | 158.7µs | 1.964ms | |
| SiLU (jit) | 110.8µs | 4.060µs | 106.5µs | 126.0µs | 208.9µs | 21.59µs | 186.4µs | 347.1µs | |
| SiLU (native) | 94.23µs | 4.252µs | 91.14µs | 111.6µs | 173.7µs | 21.12µs | 154.6µs | 303.1µs | |
| Mish (naive) | 241.1µs | 5.324µs | 235.5µs | 267.3µs | 504.7µs | 359.3µs | 463.9µs | 4.080ms | |
| Mish (jit) | 195.0µs | 6.865µs | 189.4µs | 244.7µs | 261.5µs | 9.261µs | 254.0µs | 294.9µs | |
| Mish (cuda) | 118.8µs | 4.640µs | 115.7µs | 149.5µs | 205.0µs | 75.83µs | 173.1µs | 840.7µs | |
| bfloat16 | ReLU | 85.61µs | 3.666µs | 83.97µs | 102.4µs | 171.5µs | 13.31µs | 149.5µs | 206.8µs |
| Leaky ReLU | 91.97µs | 66.68µs | 79.87µs | 754.7µs | 209.2µs | 268.3µs | 151.6µs | 2.597ms | |
| Softplus | 99.76µs | 1.696µs | 98.30µs | 106.5µs | 159.5µs | 16.70µs | 146.4µs | 275.5µs | |
| SiLU (jit) | 182.8µs | 5.078µs | 177.2µs | 205.8µs | 568.9µs | 122.0µs | 541.7µs | 1.560ms | |
| SiLU (native) | 88.71µs | 2.927µs | 86.02µs | 103.4µs | 171.5µs | 13.83µs | 147.5µs | 228.4µs | |
| Mish (naive) | 243.1µs | 4.139µs | 239.6µs | 260.1µs | 482.6µs | 177.1µs | 458.8µs | 2.214ms | |
| Mish (jit) | 259.7µs | 33.09µs | 252.9µs | 584.7µs | 781.3µs | 191.0µs | 759.8µs | 2.681ms | |
| Mish (cuda) | 259.7µs | 33.09µs | 252.9µs | 584.7µs | 781.3µs | 191.0µs | 759.8µs | 2.681ms | |
| float32 | ReLU | 129.4µs | 3.984µs | 126.0µs | 146.4µs | 220.9µs | 25.02µs | 216.1µs | 448.5µs |
| Leaky ReLU | 130.7µs | 4.009µs | 128.0µs | 148.5µs | 234.1µs | 158.8µs | 216.1µs | 1.812ms | |
| Softplus | 138.5µs | 78.90µs | 128.0µs | 922.6µs | 238.2µs | 197.8µs | 217.1µs | 2.207ms | |
| SiLU (jit) | 299.8µs | 7.123µs | 294.9µs | 341.0µs | 958.0µs | 127.0µs | 932.9µs | 1.993ms | |
| SiLU (native) | 133.1µs | 3.747µs | 124.9µs | 146.4µs | 217.9µs | 1.215µs | 217.1µs | 228.4µs | |
| Mish (naive) | 398.7µs | 55.39µs | 386.0µs | 938.0µs | 856.2µs | 243.4µs | 819.2µs | 2.613ms | |
| Mish (jit) | 407.7µs | 28.66µs | 399.4µs | 641.0µs | 1.323ms | 184.6µs | 1.295ms | 3.063ms | |
| Mish (cuda) | 142.3µs | 5.070µs | 138.2µs | 164.9µs | 281.1µs | 557.4µs | 222.2µs | 5.826ms | |
| float64 | ReLU | 326.7µs | 28.28µs | 315.4µs | 566.3µs | 497.3µs | 189.2µs | 470.0µs | 2.343ms |
| Leaky ReLU | 321.8µs | 6.283µs | 315.4µs | 349.2µs | 472.0µs | 1.451µs | 469.0µs | 479.2µs | |
| Softplus | 316.9µs | 4.720µs | 310.3µs | 335.9µs | 469.5µs | 1.753µs | 466.9µs | 478.2µs | |
| SiLU (jit) | 727.0µs | 10.50µs | 715.8µs | 786.4µs | 2.481ms | 302.3µs | 2.412ms | 4.910ms | |
| SiLU (native) | 322.0µs | 15.89µs | 316.4µs | 475.1µs | 472.8µs | 1.526µs | 469.0µs | 477.2µs | |
| Mish (naive) | 997.1µs | 18.65µs | 987.1µs | 1.176ms | 1.990ms | 3.833µs | 1.983ms | 2.002ms | |
| Mish (jit) | 1.010ms | 7.377µs | 1.000ms | 1.036ms | 3.421ms | 229.3µs | 3.378ms | 5.051ms | |
| Mish (cuda) | 346.5µs | 4.061µs | 343.0µs | 366.6µs | 471.2µs | 827.5ns | 470.0µs | 473.1µs | |
Lower is better. Bolded passes are faster than PyTorch 1.9 and italic passes are slower than PyTorch 1.9. Fastest pass and those statistically indistinguishable are highlighted. All at the p=0.001 level.
# Conclusion
Overall I am quite pleased with the performance of native Mish. On more modern hardware when training via mixed precision or full precisionUnfortunately, I did not have access to Ampere hardware, and thus was unable to benchmark Nvidia’s TensorFloat32, however I would expect it to behave similar to float16 and float32 performance. native Mish should be comparable if not faster than other native PyTorch activation functions. On older hardware native Mish is still an upgrade in performance over other Mish implementations, however Mish is no longer in contention for best performance.
The one sore spot is CPU performance where it’s best to replace the native Mish implementation with a TorchScript implementation. Hopefully future releases of PyTorch will improve Mish’s CPU forward pass performance closer to SiLU’s.
With the release of PyTorch 1.9 it is time to switch to native Mish.